When one learns mathematics, most of what one gains is knowledge how to do something: how to solve a quadratic equation, how to prove a trigonometric identity, how to find the area between the graphs of two functions, and so on.
To justify a claim that one knows how to do one of these things requires (i) a knowledge that certain truths hold, i.e. a knowledge of mathematical laws or rules, together with (ii) the ability to think logically.
Exercise 0.1.:
Someone claims that they know
how to solve the quadratic equation
x2 – x – 6 = 0 . To justify that claim, they could say that they know
that ...
- x2 – x – 6 = (x _____ )(x ______ ) , which can be checked using the distributive and the commutative law, (i.e. by 'multiplying out'.)
- If a = b and c = b , then ___ = ___ , and therefore (x ______ )(x ______ ) = 0 .
- If a b = 0 , then a = ___ or b = ___ , and therefore (x ______ ) = 0 or (x ______ ) = 0 .
- If a + b = 0 , then a = ___ , and therefore x = –2 or x = ___ .
Can you think of other ways in which the person might justify that claim?
Thus, contrary to a common misconception, doing mathematics requires not only (i) mathematical knowledge and (ii) the ability to think logically, but also (iii) the ingenuity to put that knowledge to use, to make up new arguments, to invent methods and answers: doing mathematics often involves experimenting or proceeding by trial-and-error, using one's imagination or intuition, and so on -- even if in the finished 'product', like the solution of an equation or the proof of a theorem, these processes may not be apparent. This need for ingenuity is the reason, of course, that people 'get stuck' when they do mathematics.
In a certain sense, mathematics has been advanced most by those who are distinguished more by intuition than for rigorous methods of proof.
Felix Klein (1849 --1925)
Our main concern in this section will of course with the basis on which we can claim to know mathematical truths.
But to start with, we shall take a very brief look at the two main areas into which the subject is sometimes divided.
1. Mathematics, Pure and Applied
The distinction is often made between pure and applied maths, though it would be an over-simplification to think of mathematics as divided in two.
Pure maths investigates abstract, though not necessarily 'useless', structures and the foundations of the subject. It includes areas such as set theory, theory of algebraic structures, number theory, geometry, analysis, graph theory.
- Example 1:
- A famous conjecture by Fermat (1601-65,) which has only been proved in the last couple of years, states that if n is a natural number such that n > 2, then there are no non-zero integers x, y, z such that xn + yn = zn.
- Example 2:
- The Four-Colour Theorem, which has been proved only recently as well, states that four colours will be sufficient to colour the countries on any plane map such that no two adjacent countries have the same colour.
An important concept in pure maths is that of an isomorphism (from Gk. iso- + morphé, equal shape,) when different structures agree in such a way that corresponding elements 'behave' the same way.
- Example 3:
- The set of equations of the form ax + by = c and the set of straight lines in the Cartesian plane are isomorphic, so that we can find the intersection of two lines by solving their equations simultaneously, and two lines are parallel if the corresponding equations have the same ratio a/b.
Exercise 1.1.:
- Give examples of non-zero integers x, y, z, such that x2 + y2 = z2. -- What role do such number triplets play in geometry, and what are they called?
- Draw a simple map to show that a 'Three-Colour Theorem' cannot hold.
- Considering points, line-segments and squares as 'cubes' of 0, 1 and 2 dimensions, count, for n = 0, 1, 2 and 3,
- the number of vertices of an n-dimensional 'cube',
- the number of (n -1)-dimensional sides, or 'faces', and
- the number of edges.
Try to deduce the numbers of vertices, of sides and of edges of a 4-dimensional cube -- which we can of course not imagine, but can work with mathematically.
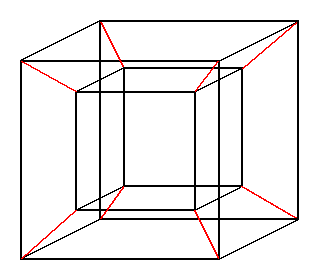 | |
Projection onto the plane of a 'wire model' of a 4-dimensional cube. |
In applied maths, theories are developed to serve as 'tools' for solving problems which arise in other areas, such as physics, engineering or economics.
As a first step, this always requires the setting up a suitable model of the situation, i.e. a simplified representation or description, by making certain assumptions about the given situation and abstracting from some of its details.
- Example 4:
- In queuing theory, which models situations of waiting in line for service, it can be shown, for instance, that when two 'phones are in one place, the average waiting time is much less than when they are in different locations.
- Example 5:
- Often the equations that describe a situation in physics, such as the movement of three bodies under the gravitational forces they exert on each other, can be set up easily enough, but can then not be solved in general.
Exercise 1.2.:
Based on your experience of different parts of the subject, what links do you think pure and applied maths may have?
2. Mathematical Proofs
In the natural sciences, as we saw, we say that we know a scientific law, such as the law of gravitation, because even though it may initially have been an invented hypothesis, the predictions we have deduced from it have been thoroughly tested in experiments, which have corroborated it; and because it is always open to further such testing.
Mathematics is not in this simple sense empirical, i.e. based on sense experience. Instead we can say that we know a mathematical truth if we know how to prove it, (which may require experience of proving things mathematically: but this is not the same as being based on sense experience.)
There are different methods of proof, classified according to the most conspicuous inference, such as
- proof by logical deduction:
- a sequence of propositions, each of which must either have been previously proved (or be evident without proof,) or follow by a valid logical argument from earlier propositions in the proof, such that the last proposition is what is to be proved.
- proof by construction:
- the objects asserted to exist are explicitly exhibited or constructed (-- which is not actually necessary to just show that they exist.)
- proof by (complete or mathematical) induction:
- in contrast to the inductive reasoning in science, this does guarantee the truth of the conclusion; it goes as follows: if a proposition p(n) depending on a natural number n is true for some first number m, and we can show that whenever p(n) is true then so is p(n+1), then p(n) is true for all n ≥ m.
- proof by contradiction:
- this works by assuming the negation of what one is trying to prove and deriving a contradiction; so the logical form of the argument is: ( ( ¨p => q ) & ¨q ) => p ;
(this is a variation of the modus tollens argument, as we saw in the section on Logic and Reasoning.)
A proof by contradiction is also called indirect, while the others are direct, and there is, or was, a school of mathematicians -- called Intuitionists -- who 'don't approve' of such indirect proofs ...
Note that methods of proof cannot be classified and catalogued easily, that there are other methods, and that many results can be proved by different methods.
Exercise 2.1.:
Try to prove each of the following propositions by the method indicated.
- 2 x2 -- 3 x = 0 has a solution between 1 and 2, (by construction.)
- There is no smallest positive number, (by contradiction.)
- n2 ≥ 2n for all n ≥ 2, (by induction.)
- 2 x2 -- 7 x + 9 / x = 0 has a solution between 1 and 2, (by deduction: clearly state all premisses of your argument.)
Exercise 2.2.:
Contrary to the practice of many IB Mathematics students, the method of the following 'proofs' is
not valid, (even when -- unlike in the cases below -- true conclusions are arrived at.) Describe the method clearly, and state which logical fallacy is committed.
The conclusions of b. and c. are clearly false; give an example of an angle P in a. for which the conclusion does not hold.
| a. |
to prove:
cos P = ÷(1 -- sin2 P)
|
b. |
to prove:
5 = 7
|
c. |
to prove:
1 = --1
|
|
square both sides:
cos2 P = 1 -- sin2 P
|
|
multiply by --1:
--5 = --7
|
|
square both sides:
12 = (--1)2
|
|
sin2 P + cos2 P = 1 -- true!
|
|
adding: 0 = 0 -- true!
|
|
so 1 = 1 -- true!
|
|
hence:
cos P = ÷(1 -- sin2 P)
|
|
hence: 5 = 7
|
|
hence: 1 = --1
|
3. The Axiomatic Approach
If we say that knowing a mathematical truth requires that we be able to prove it, then what can we base our proofs on?
We can agree that in mathematical proofs valid logical arguments are used, and perhaps also certain very basic notions, e.g. that a part cannot be greater than the whole. But it is not possible to forever keep returning to statements that have been previously proved, so mathematical proofs must be representable as consisting of inferences from statements assumed without proof. Such statements are called 'axioms' (from Gk. axioun, to consider worthy.)
The reduction of a given subject matter or theory to a set of fewer basic propositions is called an axiomatization. An example going back to antiquity is Euclidean geometry: in his famous Elements, Euclid, in the 3rd century B.C., stated five axioms, which were considered self-evident, and from these could be derived all the theorems of plane geometry. Here are some examples of axioms, (though in a modern formulation,) and a typical theorem:
| A1 | Given any two points, P and Q, there is precisely one straight line l on which they both lie. |
| A2 | Given any straight line l, there is some point P which does not lie on line l. |
| A5 | Given any straight line l and any point P which does not lie on l, there is precisely one straight line l' such that P lies on l', and l and l' have no common point. (l' is called the parallel line to l through P.) |
| T | All straight lines perpendicular to a given line are parallel. |
Similarly there are axiomatizations of set theory (Georg Cantor, 1845 --1918) and of the theory of natural numbers (Giuseppe Peano, 1858 --1932.)
Of a set of axioms we can require more than that each axiom be self-evident: the axioms should be
- consistent: it must not be possible to derive both a proposition p and its negation ¨p from the axioms;
- independent: it must not be possible to derive one axiom from the others;
- fruitful, in some sense: we would like to be able to derive many theorems from the set of axioms.
(Note that the axiomatization of a theory need not be unique, i.e. there can be different sets of axioms from which the theory can be derived: the axioms of one set are then theorems which can be proved from the axioms of the other. Thus we don't nowadays use Euclid's original five axioms as the basis of Euclidean geometry.)
We can now formulate the first of a series of views of what mathematical knowledge consists of:
|
First View:
|
|
Knowing some mathematical truth requires that we be able to prove it from a set of axioms; these axioms are self-evident in the sense that we can have immediate knowledge of them and do not need to justify them further.
|
However, in the middle of the 19th century the question was raised whether axioms needed to be self-evident, for it was found that perfectly good theories could be derived from sets of axioms which were not.
In particular Euclid's 5th axiom, A5 above, being the only one which concerned the 'global' rather than just the 'local' behaviour of the geometrical objects, had given rise to much unease amongst mathematicians; and it was found that if it was replaced by an alternative, such as A5' below, then a perfectly good non-Euclidean geometry could be derived, in which very different theorems can be derived:
| A5' | Given any straight line l and any point P which does not lie on l, there is no straight line l' such that P lies on l', and l and l' have no common point. |
| T1' | All straight lines perpendicular to a given straight line meet in one point. |
| T2' | Any two distinct straight lines enclose an area. |
It is clear that the meaning of some of the terms, such as ''straight line'', cannot be the same here as the usual, intuitive one in Euclidean geometry. But if we interpret ''straight line'' as referring to a great circle, then this non-Euclidean geometry will be the geometry of the surface of a sphere (Georg Riemann, 1826 --1866.)
While someone might object that there is no reason for studying such geometries, instead of one (Euclidean) geometry, it has in fact turned out that physical space, on the large scale, has a non-Euclidean geometry even though locally it is Euclidean.
Whereas previously the basic terms of geometry, such as ''straight line'', had been considered intuitively obvious and the axioms self-evident, the meanings of the basic terms are now defined, implicitly, by how they are used in the axioms and the theorems derived from them. This 'formalist' view goes back to David Hilbert (1862 --1943,) who is said to have commented, jokingly, that in his geometrical axioms
One must always be able to replace the words ''points'', ''straight lines'' and ''planes'' by ''tables'', ''chairs'' and ''beer mugs''.
The subject matter of mathematics is ... the concrete symbols themselves whose structure is immediately clear and recognizable.
The formal conception of numbers ... does not ask what numbers are ..., but rather what is demanded of them in arithmetic. For the formalist, arithmetic is a game with signs, which are called empty. That means they have no other content (in the calculating game) than they are assigned by their behaviour with respect to certain rules of combination (rules of the game). The chess player makes similar use of his pieces; he assigns them certain properties determining their behaviour in the game, and the pieces are only external signs of this behaviour.
J. Thomae, 1898.
Exercise 3.1.:
To understand the formalist approach, and how terms can get meaning by the way they are used, consider the formal system K which is defined by the four axioms A1 -- A4.
| A1 | Some DERs are KIN-DERs and some DERs are TEN-DERs, but no DER is both a KIN-DER and a TEN-DER. |
| A2 | The result of GARring any number of DERs is a DER, and this does not depend on the order of the DERs. |
| A3 | When two KIN-DERs or two TEN-DERs are GARred, the result is a KIN-DER. |
| A4 | When a KIN-DER and a TEN-DER are GARred the result is a TEN-DER. |
- Which of the following, if any, are theorems of the K-system? Try to derive any theorems from the four axioms above.
| P1 | When three TEN-DERs are GARred, the result is a TEN-DER. |
| P2 | When three DERs are GARred, the result is a TEN-DER. |
| P3 | Every DER is either a KIN-DER or a TEN-DER. |
- What would we say about the K-system if it included P1, P2 or P3 as a fifth axiom, A5 ?
- Try to give an intuitive mathematical interpretation of the K-system.
|
Second View:
|
|
Knowing some mathematical truth requires that we be able to prove it in its theory from the set of axioms which determines the theory; the terms used to express our knowledge have their meaning by virtue of and in the context of that theory (-- Postulationism.)
|
But even if mathematics can be thought of as a game, in which sets of axioms are invented and the theories that can be derived from them are investigated, some of these theories are of course useful:
Consider the way in which a great deal of mathematical thinking is actually done. The mathematician does not ask whether his constructions are applicable, whether they correspond to any constructions in the natural world. He simply goes ahead and invents mathematical forms, asking only that they be consistent with themselves, with their own postulates. But every now and then it subsequently turns out that these forms can be correlated, like clocks, with other natural processes.
Alan Watts.
Euclidean geometry, for instance, represents well our everyday experience of the space we live in, but a non-Euclidean geometry is needed in physics to describe the large-scale structure of space.
4. Maths and Reality
The view expressed at the end of the last section is of mathematics as a game, in which sets of axioms are developed into theories, just for their interest, though some of the theories then turn out to be of practical use.
Many mathematicians in fact view their subject in this way. However, for mathematical knowledge to be ultimately justifiable in this way would require some guarantee that our mathematical theories are 'solid': in particular, we must require the sets of axioms to be (i) consistent, i.e. free from internal contradiction, and (ii) complete, i.e. such that all the theorems of a theory can be completely derived from the axioms.
Unfortunately for the formalist view -- that mathematics is a game, albeit an at times useful one -- Kurt Gödel (1906 --1978) was able to show
- that the consistency of any formal axiomatic system (of sufficient interest) cannot be proved in that system but only in a 'larger' system, (which can of course again not prove its own consistency;) and
- that a mathematical theory, such as the arithmetic of natural numbers, cannot be completely derived from a finite set of axioms: in any such system, some statements can be neither proved nor refuted (Incompleteness Theorem.)
Gödel's proof is not easy to follow, but in the end it hinges on something like the liar's paradox known since antiquity -- Epimenides was a Cretan who is still famous for his statement: ''All Cretans are liars.''
That the consistency of mathematical theories, even ones that have become well established, cannot be taken for granted was demonstrated very clearly in 1902, when Bertrand Russell (1872 --1970) discovered a paradox (or 'antinomy') in Cantor's set theory, which had come to play a fundamental role in mathematics.
In a library there are many books, some of which are catalogues of books or even catalogues of catalogues. And a catalogue may well list itself, too. Now consider the catalogue of all catalogues that do not list themselves: does it list itself or not?
The discovery of this paradox, hidden in a well established branch of their subject, came as a major shock to the mathematical community. Here are some other, related paradoxes.
Exercise 4.1.:
Investigate the following situations.
- ''The next sentence is false. The previous sentence is true.''
- Adjectives in English can be divided into 'autological' ones, i.e. ones that are self-descriptive, such as ''pentasyllabic'', ''awkwardnessful'' and ''recherché'', and 'heterological' ones, i.e. ones that are not, like ''edible'', ''incomplete'', ''bisyllabic''. Now, is ''heterological'' heterological? (Grelling's paradox)
- The barber in a certain village is a man who shaves all men who do not shave themselves. Does the barber shave himself or not?
- If it is true that ''the class of integers which can be expressed in less than 16 words is finite,'' then there must be a ''smallest integer not definable in less than 16 words'' -- the definition of which has only ten, and therefore less than 16, words! (Berry, Russell)
One answer, put forward by W. V. O. Quine and Hilary Putnam, amongst others, comes from basing mathematical knowledge ultimately on facts of experience, like scientific knowledge.
The question of how mathematics and science are related was of great concern to Albert Einstein (1879 --1955):
Here arises a puzzle that has disturbed scientists of all periods. How is it possible that mathematics, a product of human thought that is independent of experience, fits so excellently the objects of physical reality? Can human reason without experience discover by pure thinking properties of real things? ...
As far as the propositions of mathematics refer to reality they are not certain; and as far as they are certain they do not refer to reality. ... But it is, on the other hand, certain that mathematics in general and geometry in particular owe their existence to our need to learn something about the properties of real objects.
But Einstein would probably not have been happy with the position taken by Quine, which is as follows:
When we discussed science, we saw that we can never test an hypothesis in isolation: a prediction is always derived from the hypothesis H to be tested in conjunction with some 'auxiliary hypotheses'. So if such a prediction turns out to be incorrect, it may actually be one of the auxiliary hypotheses that has thereby been disproved rather than H. But conversely, if the prediction was correct, not only has the hypothesis H been corroborated, but so have the auxiliary hypotheses involved in making the prediction.
Certain of these auxiliary hypotheses are very general, and are tested in a wide range of experiments performed to test specific hypotheses. Thus any prediction in chemistry requires us to assume that matter does not simply disappear: the law of conversation of mass is one of these very general auxiliary hypotheses, and every time an experiment turns out as predicted, this law has been corroborated as well. Even our everyday 'predictions' of the outcomes of 'experiments', as when we are cooking, corroborate the law -- so we are very sure of it.
Exercise 4.2.:
To see what such very general auxiliary hypotheses are, decideˇwhat assumptions you would be prepared to reject if the following things happened, and which ones you wouldn't.
- Having put together two amoebas and two amoebas in a petri dish, you then count five amoebas. (Is therefore 2 + 2 = 5 ?)
- You put together two apples and two apples and later find that there are only three apples. (Is therefore 2 + 2 = 3 ?)
- Mixing 1 pint of a liquid with 1 pint of another liquid gives you a volume of 1.9 pints.
- A and B are twins. A goes on a space trip far away while B stays behind. When A returns she is considerably younger than B.
This has also been put as follows, and can be formulated as our third and final view of what mathematical knowledge consists of.
we regard our knowledge of basic principles [of mathematics] as resting on the wide-spread application of such principles in theories from the natural or social sciences which are in turn confirmed via sensory observations. In other words, ... basic mathematical principles are known via an inferential process which accords well with the hypothetico-deductive patterns [of the sciences.]
Hugh Lehman.
Why do we not confess that mathematics, like other sciences, is ultimately based upon and has to be tested in practice?
Lazlo Kalmar.
|
Third and Final View:
|
|
Knowing some mathematical truth requires that we be able to prove it in its theory; what constitutes a proof, and the foundations of some theories, have been tested, in conjunction with specific hypotheses, in science, and often in everyday life. Our knowledge of other parts of mathematics is less conclusive the further it is from what has been so tested.
|
Exercise 4.3.:
There are various points at which a relation between mathematics and reality can give us a surprise:
Count in a variety of tables and lists -- in the Encyclopaedia Britannica, say, or geography books, balance sheets in economics, astronomy books, etc. -- how many numbers start with each of the digits 1, 2, and so on, up to 9, (excluding any that follow a definite pattern, such as dates and page numbers.)
Try to explain why the distribution is not even, i.e. why the proportion for each digit is not 1/9, as one might have expected it to be. (The pattern is called Benford's Law.)
Discussion:
It has been said, often unthinkingly, that ''mathematics is a language.'' By considering carefully how a language functions, what we use it for, how we learn it, and so on, find ways in which mathematics is, and is not, like a language.
Teaching Notes :
1. Mathematics, Pure and Applied :
Exercise 1.1.:

- Using only three colours, there is for example no way of colouring the four countries on the imaginary island on the right in such a way that no two countries with the same colour share a border.
-
| vertices
vn = 2 ∑ vn-1 | faces
fn = fn-1 + 2 | edges
en = 2 ∑ en-1 + vn-1 |
| point: | 1 | 0 | 0 |
| line segment: | 2 | 2 | 1 |
| square: | 4 | 4 | 4 |
| cube: | 8 | 6 | 12 |
| 4-D cube: | 16 | 8 | 32 |
Even though we cannot imagine a 4-D cube, we can draw a projection of a wire model of one in 2-D, just as we can draw the projection of a wire model of a 3-D cube:
- line segment: draw two points, and connect them with a straight line;
- square: draw two line segments, (one above the other,) and connect the ends with straight lines;
- cube: draw two squares, (one shifted up a little and to the right of the other,) and connect corresponding vertices with straight lines;
- 4-D cube: draw two cubes, (one smaller and inside the other,) and connect corresponding vertices with straight lines.
(This exercise works even more easily with the following sequence: point, line segment, triangle, tetrahedron, and 4-D tetrahedron.)
2. Mathematical Proofs :
Exercise 2.2.:
This method starts by assuming the proposition to be proved, and then deduces from it a proposition which has previously been proved (or is evident without proof.)
The form of the argument is:
( ( p => q ) & q ) => p ,
which is a case of 'affirming the consequent', a logical fallacy.
In a., if one starts with sin2 P + cos2 P = 1 , as one should, all that one can in fact deduce is that cos P = Ī ÷(1 -- sin2 P) .
3. The Axiomatic Approach :
Exercise 3.1.:
- When two TEN-DERs are GARred the result is a KIN-DER (by A3,) and when this is GARred with another TEN-DER, the result is a TEN-DER (by A4,) so P1 is a theorem. P2 and P3 do not follow from the axioms.
- Including P1 : the axioms of the K-system would not be independent (-- see a.)
Including P2 : it already follows from A1 -- A4 that when three KIN-DERs are GARred, the result is a KIN-DER, so the axioms would be inconsistent.
Including P3 : we would get a different formal system.
- The K-system is 'isomorphic' with the odd and even numbers under addition, and with positive and negative numbers under multiplication: two minuses make a plus, etc.
4. Maths and Reality :
Exercise 4.2.:
- Reject conservation of amoeba number, but not conservation of mass, or that 2 + 2 = 4.
- Reject my ability to count, or the assumption that there are no hungry thieves around, but not conservation of mass, or that 2 + 2 = 4.
- Reject conservation of volume, but not conservation of mass. (This 'shrinking' happens when alcohol and water are mixed, for instance.)
- Reject simultaneity, but not the working of the biological clock. (The twin-paradox is a well-known result of relativity theory.)
Exercise 4.3.:
While one might expect the distribution to be even, i.e. each digit to occur in 1/9 = 11.1 % of the cases, it will in fact be found to be very uneven and something close to the following:
| first digit |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| proportion (%) |
30.1 | 17.6 | 12.5 | 9.7 | 7.9 | 6.7 | 5.8 | 5.1 | 4.6 |
One explanation -- the only one I have been able to come up with ... -- starts from the requirement that the distribution must be such as to be independent of the units of measurement used: whether we measure population by counting the individuals, say, or the number of their limbs, or measure area in m2 or in m2/2.
It can then be shown that the proportion of numbers starting with the digit n is p(n) = log (n+1) -- log n .
Reading :
Walter R. Fuchs,
Modern Mathematics, 1966. Weidenfeld and Nicolson.
Behnke et al. (editors), Fischer Lexikon Mathematik, 2 vol.s, 1964. Fischer Bücherei.
Douglas R. Hofstadter, Gödel, Escher, Bach, 1979. Vintage Books.
Hugh Lehman, Introduction to the Philosophy of Mathematics, 1979. Basil Blackwell.
Andrew Maclehose, Th.o.K. Notes on Mathematics.

